

澳门太阳网城官网周岱教授团队研究成果近日在流体力学权威期刊《Journal of Fluid Mechanics》发表,该成果主要涉及圆柱尾流控制及其稳定性的研究新进展[J. Fluid Mech. (2019), vol. 874, pp. 299-338]。论文以包艳副研究员和周岱教授为共同通讯作者,在读博士生王锐为第一作者,韩兆龙等团队其他几位师生和航空航天学院徐辉副教授为共同作者,巴西圣保罗大学D. Serson博士为国际合作者。流体力学期刊是传统流体力学领域的Top 1期刊。
工程界和自然界广泛存在尾流现象。流体流经圆柱(如深海立管)产生尾流,圆柱因流动分离和旋涡脱落而承受周期性动力作用,由此诱发的复杂涡激振动引起圆柱结构疲劳损伤甚或动力灾变。研究如何有效抑制圆柱尾流及涡激振动具有重要的学术价值和应用意义。接触式平行分隔板作为圆柱尾流控制的新型装置,其抑制效果和水动力性能优于传统分隔板,已引起国内外广泛关注。然而,该装置对尾流性态和尾流不稳定性的影响,目前知之甚少。
针对上述科学问题,研究团队系统性研究了配置接触式平行分隔板圆柱系统的尾流特性规律、分隔板对圆柱尾流控制和尾流转捩的影响机制。采用高精度谱单元数值方法并通过Floquet线性稳定性分析,细致观察到分隔板显著改变了圆柱尾流拓扑结构,首次发现尾流通过两个全新的二次不稳定性路径发生转捩即模态A′ 和模态B′(图1)。分析发现,模态A′ 产生的物理机制可能是椭圆不稳定性(elliptic instability),而模态B′ 的物理机制是双曲不稳定性(hyperbolic instability)。上述模态不稳定性特征与经典圆柱尾流转捩方式完全不同。随着分隔板板长增加,原有不稳定性(即模态A,B和QP)虽被抑制,但这两种新的不稳定模态对三维扰动的演化发展仍发挥主导作用。基于Landau非线性理论,发现这两种二次不稳定性模态均为超临界霍普夫分叉(supercritical Hopf bifurcation),但强度差异巨大(图2)。上述成果丰富了对圆柱尾流二次不稳定性等流体力学经典问题的研究,对研发深海立管减振装置有重要理论指导意义。

图1. (a) 两种新的二次不稳定性的中性曲线; (b) 模态A′ 的三维结构; (c) 模态B′ 的三维结构
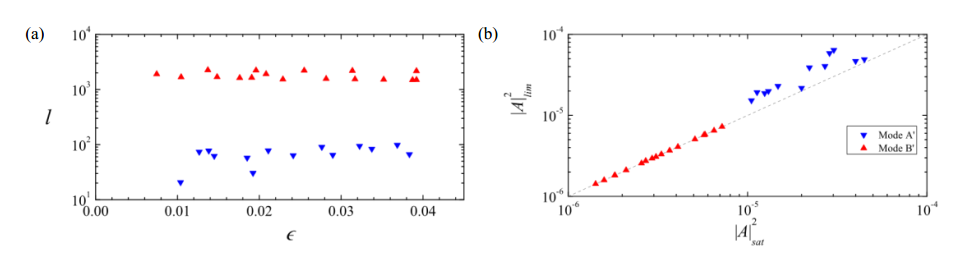
图2. 两种新二次不稳定性非线性分析:(a) Landau方程系数l; (b) Landau方程预测幅值和直接数值模拟结果的对比
该项工作得到国家自然科学基金、上海市科委和上海市教委等研究项目的资助。
论文链接:http://dx.doi.org/10.1017/jfm.2019.439
文/包艳