

著名的三体问题可追溯到17世纪的牛顿, 以及其后的拉格朗日、欧拉、庞加莱等知名科学家。三体问题的研究, 导致庞加莱发现混沌动力系统对初始解的极端敏感性。相对论、量子力学和混沌动力学的创立被认为是20世纪物理学最伟大的三次革命。因此, 三体问题的研究具有重要的科学意义。
庞加莱发现, 三体问题的轨道通常都是非周期的。因此, 发现三体问题周期解具有重要科学价值。但遗憾的是, 在牛顿提出三体问题之后的三百年内仅发现3类周期解。这也充分说明了获得三体问题周期解之困难。2013年, 塞尔维亚物理学家做出重大突破, 采用计算机数值模拟发现了三体问题11个新周期解家族。近来, 上海交通大学廖世俊研究小组利用超级计算机和一种全新数值模拟策略, 发现了三体问题600多个全新的周期解家族, 其结果于2017年9月在Science China-Physics, Mechanics & Astronomy第60卷第12期在线发表。
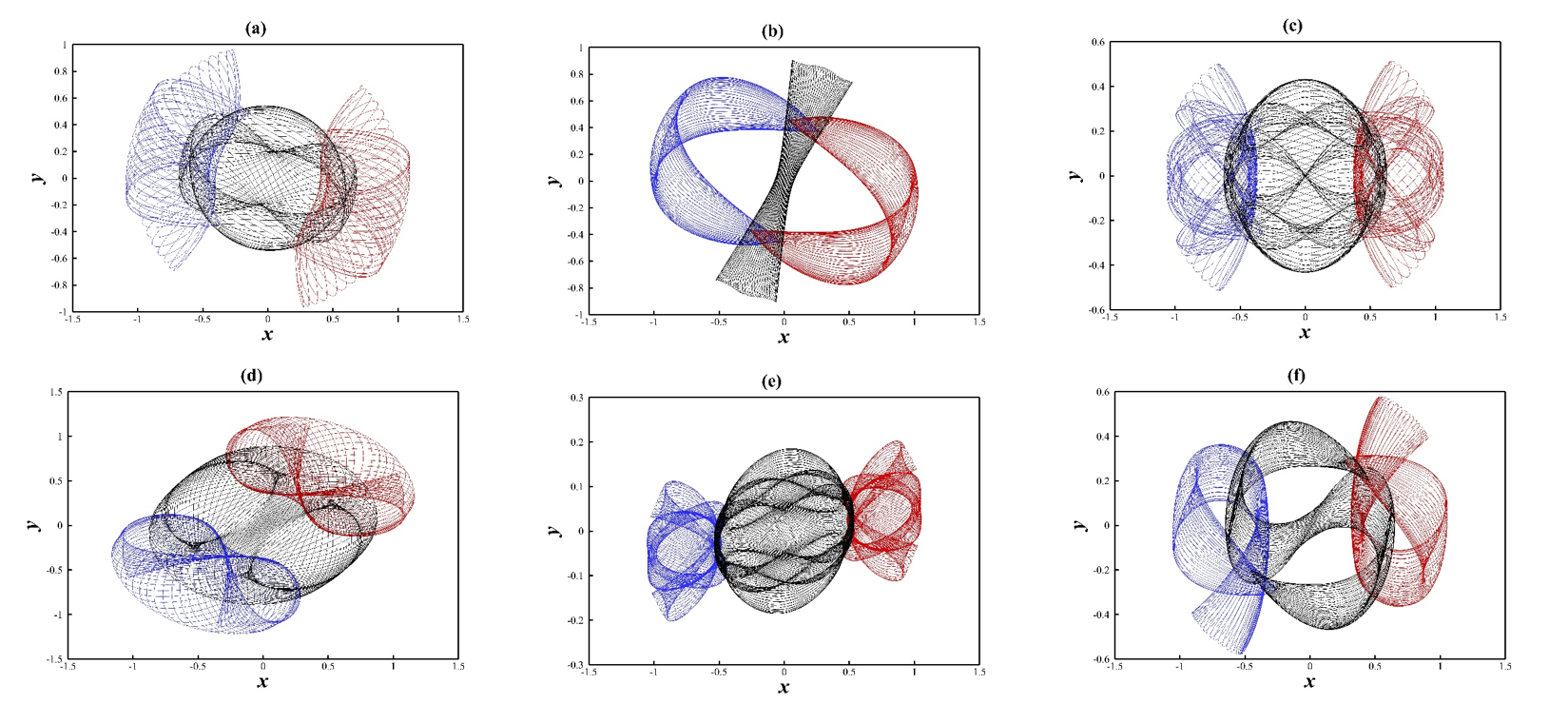
该研究小组共获得695个三体问题周期解家族, 不仅包含之前已知的周期解, 而且有600多个周期解从未见报道。该文第一作者为李晓明(博士研究生), 其通讯作者为廖世俊教授。他们研究了两维平面内等质量的三个物体在牛顿万有引力作用下的周期轨道问题, 寻找该系统角动量为零条件下其周期轨道所对应的初始位置和速度。为了克服众所周知的三体问题轨道计算对初始条件的极端敏感性, 他们首次采用廖世俊教授2009年提出的求解混沌动力系统可靠轨迹之计算方法 —— “精准数值模拟”(Clean Numerical Simulation, 简称CNS), 通过采用足够高阶的泰勒级数和足够多字长的多倍精度(Multiple Precision)数据, 大大降低截断误差和舍入误差, 使数值噪音在求解的时域内可以忽略不计, 从而成功获得该三体问题更多的周期解。其数值模拟在天河2超级计算机上完成, 共进行了一千六百万次搜寻计算。
众所周知, 两体问题的轨迹为椭圆, 且满足著名的开普勒定理: 绕以太阳为焦点的椭圆轨道运行的所有行星, 其各自椭圆轨道半长轴的立方与周期的平方之比是一个常量。该研究小组首次发现, 该三体系统695个周期解满足一个广义的开普勒定理: 整个系统动能和势能之和的立方与平均周期的平方之乘积几乎是一个常量。这首次揭示了三体系统的一个共性, 深化了对三体问题的全面理解。
该论文的作者认为, “三体问题这些新周期解的发现, 主要归功于计算机技术的发展和新的数值模拟策略(CNS)之应用”; “三体问题许多新发现的周期解非常美, 简直可以作为现代艺术画挂在墙上。这种完美令人震惊和着迷”。